| University | Singapore University of Social Science (SUSS) |
| Subject | BM1776: Inventory and Cost Management |
Assignment 1 – Case Study (Individual Assignment)
Dynamic Lot Sizing
The dynamic lot-size model in inventory theory, is a generalisation of the Economic Order Quantity (EOQ) model that takes into account that demand for a product varies over time.
Dynamic lot sizing sometimes refers to as ‘Time-Varying Demand’ as well. In contrast to EOQ model where demand is constant, in the time-varying deterministic demand model, demands of various periods are unlike. The variations depend on different reasons. For example, production on a contract, which requires that certain quantities are delivered on specified dates. Note that we are still considering deterministic demand, i.e., all variations are known in advance.
In the basic models, lead-time is disregarded. When dealing with lot sizing for time-varying demand, it is generally assumed that there are a finite number of discrete time steps, or periods. A period may be, for example, a day or a week. We know the demand in each period, and for simplicity, it is assumed that the period demand takes place at the beginning of the period. There is no initial stock. When delivering a batch, the whole batch is delivered at the same time. The holding cost and the ordering cost are constant over time. No backorders are allowed. We shall use the following notation:
Var Definition
𝑇 = number of periods,
𝑑𝑖 = demand in period i, 𝑖 = 1, 2, …, 𝑇 ,
𝑂𝐶 = ordering cost,
𝐻𝐶 = holding cost per unit and time unit.
Hire a Professional Essay & Assignment Writer for completing your Academic Assessments
Native Singapore Writers Team
- 100% Plagiarism-Free Essay
- Highest Satisfaction Rate
- Free Revision
- On-Time Delivery
Problem
Costco has received the following demands for a product this year:
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Demand | 300 | 700 | 800 | 900 | 3300 | 200 | 600 | 900 | 200 | 300 | 1000 | 800 |
Suppose ordering cost (OC) is $504 and holding cost (HC) of one unit of product in a year is $3.
There is no shortage cost. Backordering is not allowed in this model.
To achieve the minimum total cost (ordering cost + holding cost), how many times the company should place orders in a year? In each order, how many products should be ordered? What is the total cost in a year?
Watch
Watch these two videos:
• Video 1: Lot Sizing
• Video 2: Lot sizing – heuristics
Questions
Q1 (2 marks)
Given that the total demand of the whole year is 10,000 products, suppose the company is going to use the EOQ model for the accumulated demand of one year (10,000). In other words, ignore the monthly demand. Compute:
• Optimal order quantity (Q*)
• Total cost
• Frequency of orders
• Time between orders
Q2 (5 marks)
Use mixed integer linear programming to solve the problem regarding the monthly demand. Suppose that holding cost is applied to the ending inventory.
• Develop the mathematical model in the Word document.
• Solve the problem in Excel
• Develop a plan in the Word document and explain when and how many products should be ordered in order to minimise the total cost.
• Recalculate the optimal value of objective function (total cost with the new assumption that the holding cost is applied to the average inventory (not ending inventory).
Q3 (1 mark)
Use ‘Lot for Lot’ heuristic method and compute the total cost.
Q4 (3 marks)
Use ‘Part Period Balancing’ heuristic method, develop a schedule to show when and how many products should be ordered, and compute the total cost.
Note: to compute holding cost, use average inventory (not ending inventory)
Q5 (4 marks)
Use ‘Silver_Meal’ heuristic method, develop a schedule to show when and how many products should be ordered, and compute the total cost.
Silver Meal heuristic method was coined by Gorham (1968).
Note: to compute holding cost, use average inventory (not ending inventory).
Buy Custom Answer of This Assessment & Raise Your Grades
Q6 (3 marks)
Over the last five questions, you applied the methods which were explained in the videos. Now, it is your turn to research!
In this section, students are required to use Dynamic Programming based on the ‘Wagner-Whitin’ Algorithm to develop a schedule to show when and how many products should be ordered, and compute the total cost.
To understand how Wagner-Whitin Algorithm works:
• Refer to the chapter ‘Single-Echelon Systems: Deterministic Lot Sizing’, section 4.6 (The Wagner-Whitin Algorithm works:) of Axsater’s book (Axsater, 2007) which is available online via RMIT library.
• Check slides 14 to 18 of this reference in which a sample problem is solved using the Wagner-Whitin Algorithm.
If you are interested to read the original article (Wagner and Whitin, 1958), you can click here.
Note: In the process of identifying the optimal order quantity, use the ending inventory. Then, to compute the total cost, use average inventory (not ending inventory).
Summary (2 marks)
Put the results of all methods in a summary table (template is provided as below), and discuss.
| Method | Number of Orders | Months that an Orders are Placed | Total Holding Costs | Total Ordering Cost | Total Cost |
| 1. EOQ | |||||
| 2. MILP bsed on Ending Inventory | |||||
| 3. MILP bsed on Average Inventory | |||||
| 4. Lot for Lot heuristic | |||||
| 5. Part Period Balancing heuristic | |||||
| 6. Silver_Meal heuristic | |||||
| 7. Wagner-Whitin Algorithm |
Note
• For all questions, the answers should be provided in the Word document. However, it is only mandatory to provide your solution in Excel for the Linear Programming section.
• The process and calculation steps should be included in the Word document.
Rubric
Please refer to the end of this document.
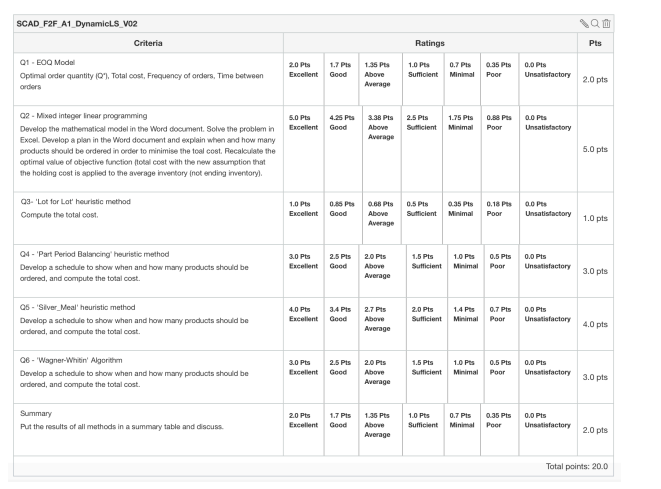
Rubric of Assignment 1
References
Axsater, S. (2007) Inventory control. Second Edition. Boston, MA: Springer US (International series in operations research & management science).
Gorham, T. (1968) ‘Dynamic order quantities’, Production and Inventory Management, 9(1), pp. 75–81.
Wagner, H. M. and Whitin, T. M. (1958) ‘Dynamic version of the economic lot size model’, Management science. INFORMS, 5(1), pp. 89–96.
Stuck with a lot of homework assignments and feeling stressed ? Take professional academic assistance & Get 100% Plagiarism free papers
Looking for Plagiarism free Answers for your college/ university Assignments.
- SWK352 Tutor-Marked Assignment SUSS January 2025 : Children And Their Issues
- COS364 Tutor-Marked Assignment (TMA) SUSS January 2025 : Interventions for At-Risk Youth
- FMT309 Tutor-Marked Assignment (TMA01) SUSS January 2025 : Building Diagnostics
- HFS105 Tutor Marked Assignment 02 SUSS January 2025 : Cognition and Information Processing
- SUSS : Legal Liability in Adventure Tourism A Case Study Analysis
- BSL202 TJA, 2025 SUSS : Workplace Law Employment Classification and Contractual Obligations
- Ethical Theories and Contemporary Business Issues: Coursework Re-Assessment
- MTD220 ECA January 2025 SUSS : User Experience (UX) Design and Web Technologies
- FMT101 TMA01 January 2025 SUSS : Building Services
- LAW 2629 Semester 1 2025 Individual Assessment SUSS :Singapore Company and Finance Law

