Question 1:

A bathroom floor needs to be tiled. Each tile is a 2 × 1 rectangle. However, the floor contains obstructions like the drain, sink, toilet, bath, and cupboard that cannot be tiled over. Suppose you are given this information about the bathroom floor layout in an n × m grid P of unit squares where P[i][j] denotes if there is no obstruction in that unit square (true if there is no obstruction, and false if there is an obstruction). Design an algorithm to determine if the floor can be tiled without cutting any of the tiles.

a) Describe an efficient algorithm to solve this problem.

b) Analyze the time complexity.

Question 2:

Consider the flow network below, where x/y denotes x as the flow value and y as the edge capacity.

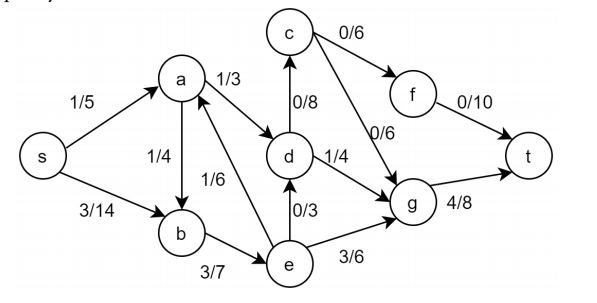
a) Trace the Ford-Fulkerson algorithm on this network. Draw the residual graph and the augmenting path on each iteration.

b) Prove that the flow you obtained from the algorithm is a max flow.

c) If the edge capacity of e-g was increased from 6 to 7, would the max flow change? Why or why not? What would the new value be?

Question 3:

You are a gardener working on a large estate. There are n plants available to be planted in k garden beds. Each plant has a beauty rating b1, b2, b3…..bn. In order to maximize the diversity of plants and obtain the most beautiful garden as a whole, the BEST-GARDEN LAYOUT problem finds an allocation of plants maximizing the beauty of the least-beautiful garden bed (sum of the beauty ratings of its plants).

Consider the decision version of this problem, that is, BEST-GARDEN-LAYOUT returns TRUE if there is an allocation of plants where the least-beautiful garden bed is at least L, otherwise FALSE.

The inputs are:

• a list of n non-negative integers (beauty ratings for plants),
• the number of garden beds k,
• a lower bound L

a) Prove that BEST-GARDEN-LAYOUT is in NP.

b) Prove that PARTITION ≤p BEST-GARDEN-LAYOUT. Note that both of these problems are decision problems.

Question 4

Your friend is developing a board game. They have come up with the following design of the board as below, it is a sequence of integers in a row coloured either green or red.

Each player has a token they can use to move around the board. The rules are as follows:

• The player can choose any square to start.
• If the square is green, they must move right (by any number of squares) to a square with a number greater than their current one.
• If the square is red, they must move left (by any number of squares) to a square with a number greater than their current one.
• This is repeated until no moves are available, then the player is finished.
• When all players are finished, the player who had the most moves wins

Your task is to design an algorithm using dynamic programming to always win this game, given a specified board layout as input. Namely, your algorithm will receive an array of n integers A[0…n − 1] and an array of n colors C[0…n − 1] ∈{r,g}, corresponding to the integer in the cell with the same index. Your algorithm should return a sequence of indices I[0…k − 1] which represents the longest sequence of moves possible in the game (the indices of the cells where the player places their token in the order in which it is done).

More formally, it is the longest sub-sequence of the board layout satisfying:

• 0 ≤ I[j] ≤ n − 1 for all j.
• A[I[j]] < A[I[j + 1]] for all j < k.
• If C[I[j]] is green, then I[j + 1] > I[j].
• If C[I[j]] is red, then I[j + 1] < I[j].

If there are multiple such sequences of the same length that are longest, your algorithm may return anyone. In the initial example, a result would be:

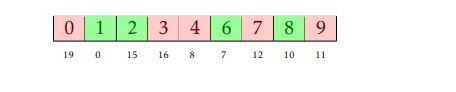
(The small numbers are the indices in the array A, which is what is actually returned by the algorithm.)

Further Examples:

Input: A=[9, 6, 9, 3, 8, 9, 2, 0, 4, 12]
Output: [7, 6, 3, 8, 1, 4, 0]

Input: A=[1, 2, 3, 4, 5, 6, 7, 10]
Output: [7]

Input: A=[5, 3, 2, 0, 24, 9, 20]
Output: [0, 5, 4]

a) Describe your algorithm. Define the DP states, state and justify the recurrence (base and recursive cases).

b) Analyse the time complexity.

c) (Optional) Implement your algorithm on Edstem.