ECON104: 1 Chapter 2 Equilibrium Analysis Consider the demand and supply curves: Mathematics for Economics Homework, SMU, Singapore

Homework 1. Chapter 2 – Equilibrium analysis

1. a. Consider the demand and supply curves

where  and  are suitable positive constants.

a. Find the equilibrium price P*, and the corresponding quantity Q*.

b. Suppose a tax of $ per unit is imposed on the producer. Find the new equilibrium price. How does it change?

c. Compute and compare the total revenues obtained by the producer before the tax is imposed (R*) and after (Rˆ).

d. Use diagrams to illustrate the difference between the two market equilibria (with and without the tax).

2. a. Given  = –
0 0 0
4 0 0
10 5 0
2, find # , $ ,   + # and where denotes the identity matrix of order 3.

b. Use the results in (a) to find ( − )%&.

3. Let  be the n × n matrix where all the elements are 1.

a. Show that  for all real numbers a and b.

b. Use the result in (a) to find the inverse of  = –
4 3 3
3 4 3
3 3 4

4. Let the IS equation be where 1 – b

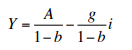
is the marginal propensity to save, g is the investment sensitivity to interest rates, and A is an aggregate of exogenous variables.

Let the LM equation be

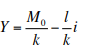
where k and l are income and interest sensitivity of money demand, respectively, and M0 is real money balances.

a. Write the IS-LM system in matrix form, with Y and i as endogenous variables.

b. Solve for Y and i (by any methods)

5. a. Find the values of p and q for which the equation system
x1 + x2 + x3 = q
px1 + x2 − x3 = 5
x1 − x3 = p
has:

(i) one solution; (ii) several solutions; (iii) no solution.

b. Find an expression for the general solution of the system in case (ii).

6. Consider a three-sector input–output model in which sector 1 is agriculture, sector 2 is manufacturing, and sector 3 is energy. Suppose that the input requirements are given by the following table:

Now suppose that final demands for the three goods are 100, 80, and  units ( > 0),
respectively. If x1, x2, and x3 denote the number of units that have to be produced in the three sectors,

a. Write down the Leontief equation system for the problem.

b. What are the values of  and  that give the system unique solution.

7. For each real number , let

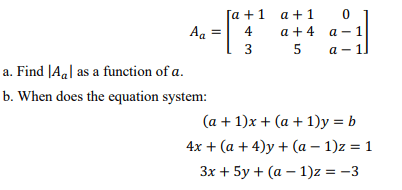
a. Find |(| as a function of .

b. When does the equation system:

have a unique solution? (You need not find the solution.)

c. Specify the conditions that b must satisfy for the system to have any solution when: