Question 1

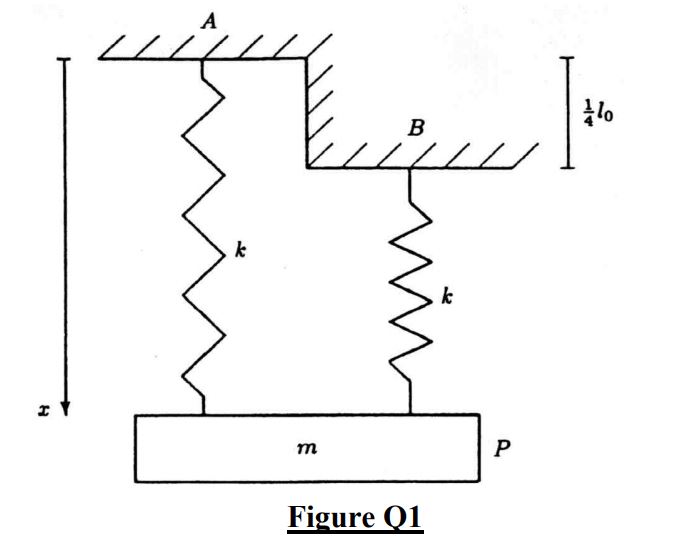
A particle P of mass m is attached to two fixed points A and B by two identical model springs of stiffness k and natural length l0. The point A is at a height 41 l0 above point B. The particle is free to oscillate vertically under gravity and both springs remain vertical throughout the motion, as shown in the diagram. Air resistance may be neglected.

(a) Choose an appropriate coordinate system to describe the motion of this system, and draw a force diagram indicating all the forces acting on the particle.

(b) Determine all the forces, in vector form, acting on the particle P when it is at a distance x below the fixed point A.

(c) Apply Newton’s 2nd Law, derive the equation of motion of the particle.

The stiffness of the springs is k = 4 mg/l0.

(d) Find a general expression (containing two arbitrary constants) for the particle’s position x at time t.

(e) Find the period of the particle’s oscillation.

(f) Find the position at which the particle can remain in equilibrium. Now, consider afresh the system described earlier for the case k = 4 mg/l0 except that now, the principle of the conservation of mechanical energy is applied.

(g) Apply energy principles, find an expression for the total mechanical energy of the system when the particle P is at a distance x below the fixed point A. The particle P is initially released from rest a distance l0 below point A.

(h) Find the speed of the particle when it is at a distance 4 5 l0 below point A.

(i) Find the positions of the particle P when it is instantaneously at rest in its subsequent motion.

Question 2

This problem describes Newtonian mechanics in more than one dimension. Peter, imprisoned in a cell, wishes to get a message to his messenger who is loitering outside a wall surrounding his prison. Peter has wrapped his message round stone and intends to throw it from his prison cell window, over the wall, to the land where the messenger can retrieve it. Peter can throw the stone at 16 ms-1. The cell window from which he can throw the stone is 6 m above the level ground outside the prison. The wall rises 10 m above the ground outside the prison and is at a horizontal distance of 20 m from Peter’s cell window. The stone has a mass 0.2 kg.

(a) Suppose that Peter throws the stone at an angle of 9 2π radians (40 0) above the horizontal. Describe whether the stone will clear the wall, neglecting air resistance.

(b) Analyze what range of launch angles will enable Peter to get the stone over the wall, if air resistance can be neglected?

(c) Peter wants to throw the stone so that it lands as far as possible from the wall, to reduce the chances of the messenger being detected as he searches for it. Describe what launch angle should he choose (still neglecting air resistance and stone must clear the wall)? For this launch angle, analyze how far beyond the wall will the stone land?

Question 3

A fish tank in a house has the following internal dimensions: it is 75 cm long, 30 cm wide and 35 cm deep. It is made of glass 4 mm thick and is filled with water to the top. Both its top and its bottom are sufficiently well insulated that it can be assumed that no heat escapes from either. The air in the room in which the fish tank stands is maintained at a constant temperature.

Heat is transferred from the water in the tank to the surrounding air by convection at the surface between the water and the glass, by conduction through the glass, and by convection at the surface between the glass and the air.

The convective heat transfer coefficient for convection at the surface between water and the glass to be 1000 Wm-2K-1; the convective heat transfer coefficient for convection between the glass and the air to be 10 Wm 2K-1, and the thermal conductivity of glass to be 1.0 Wm-1 K-1.

(a) Show that the rate q of heat transfer from the water to the air may be expressed as q = B(θ – θair), where θ is the water temperature, θair is the air temperature, and B is a constant.

Determine an expression for B in terms of appropriate parameters (which should be clearly defined), and state its units. Hence, find the numerical value of B.

(b) Interpret the power the heater consumes if the temperature of the water is maintained at a constant 26 0 C when the temperature of the surrounding air is a constant 18 0 C.

(c) Now, the heater fails for any reason, interpret that after the heater fails the temperature of the water satisfies the differential equation

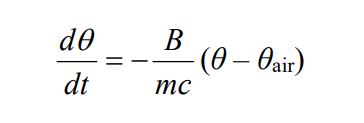
where t is the time since the heating was turned off, in seconds, m is the mass of the water, in kg, and c is the specific heat capacity of the water in J kg-1 K-1.

(d) The fish will die if the water temperature falls below 24 0C. Find the time where the fish can survive the failure of the heat supply if the water temperature is 26 0C when the heater fails and the air temperature is 18 0C? (The density of water is 998 kg m-3 and its specific heat capacity is 4190 Jkg-1 K-1.)

(e) If the tank had larger dimensions, interpret would the time is taken for the temperature to drop from 26 0C to 24 0C be longer or shorter? Justify your answer.

Question 4

A pendulum consists of a particle P of mass m attached to a model string of length l. The other length of the string is attached to a fixed point O and the particle moves in a vertical circle about this fixed point.

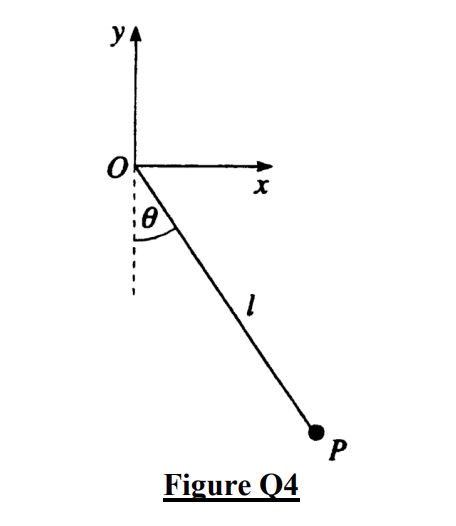
The angle θ made by the string with the vertical is measured anticlockwise and we assume that the only forces acting on the particle are its weight W and the tension force T due to the string. The particle starts at its lowest point, with horizontal speed v0 = 7gl / 2 in the anticlockwise direction.

(a) Describe the value of the angle θ for which the magnitude of the tension force T becomes zero. (State clearly which formula in the unit you have used to derive your result.) What physically happens at this point?

(b) Show that the speed V of the particle when the tension becomes zero is given by V = gl / 2. (Again clearly state which formula in the unit you have used to derive your result.)

(c) Take the point O as the origin, with the x-axis horizontal and the y-axis vertical as shown in the figure. Let i and j be unit vectors in the positive x- and y-directions respectively. Show that the position of the particle when the tension becomes zero is l 2 1 ( 3 i + j) and that the velocity at this point is 2V1 (-i+ 3 j).

(d) We take time t = 0 at the moment when the tension becomes zero. In its subsequent motion, the particle behaves for a time like a projectile. Describe a formula for r(t), the subsequent position of the particle, in terms of t, l, and g, the acceleration due to gravity.

Question 5

This problem describes a rigid body rotation. A uniform rod of mass m and length 2a is held so that one-third of its length rests on a horizontal table at right angles to an edge, the other two-thirds projecting beyond the edge. It is then released from rest. The rod will rotate about an edge at O through an angle θ before it begins to slip as shown. The coefficient of static friction between the rod and the edge is μ.

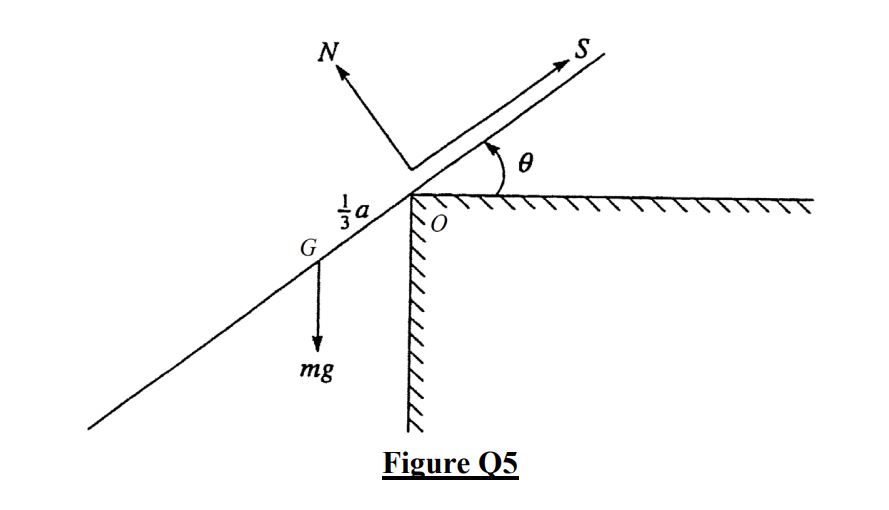
(a) Implement the parallel axis theorem, find the moment of inertia of the rod of length 2a about an axis perpendicular to the rod and through a point O, one third from one end. [Given IG = 121ml2, where l is the length of the rod]

(b) Implement the conservation of mechanical energy to show that while the rod is rotating without slipping about the edge of the table,

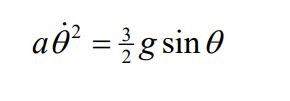
where g is the magnitude of the acceleration due to gravity.

(c) The reaction of the edge on the rod has two components, namely the frictional component of magnitude S preventing slipping, and the normal component of magnitude N acting perpendicular to the rod. By implementing the general equation of circular motion of the rod’s center of mass G, show that

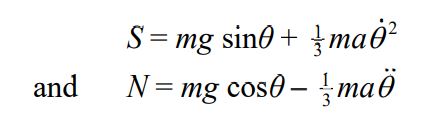
while the rod is rotating without slipping.

(d) By using the equation derived in part (b) express S and N in terms of m, a, g and θ